Bootstrapping
How to use your data to get out of a tight spot
Peter Humburg
21 October 2021
The Problem

Failing assumptions
- Many statistical test rely on assumptions about distributions
- Often: Test statistic is normally distributed
- Real world data may differ
- Sometimes can use non-parametric alternatives
- but options are limited for complex analyses
It’s even worse
- Assumptions often don’t relate to the data directly
- t-test: The sample mean is normally distributed
not: The observations are normally distributed
- t-test: The sample mean is normally distributed
- Only have one sample. How do you know about the distribution of the mean?
Usually you don’t have to worry too much, especially if the distribution of the data is vaguely symmetric. But here we are interested in situations where we do need to worry.
Bootstrapping

Working with what we’ve got
- Idea: We have sample from the population we want to study, can we just create more samples from that?
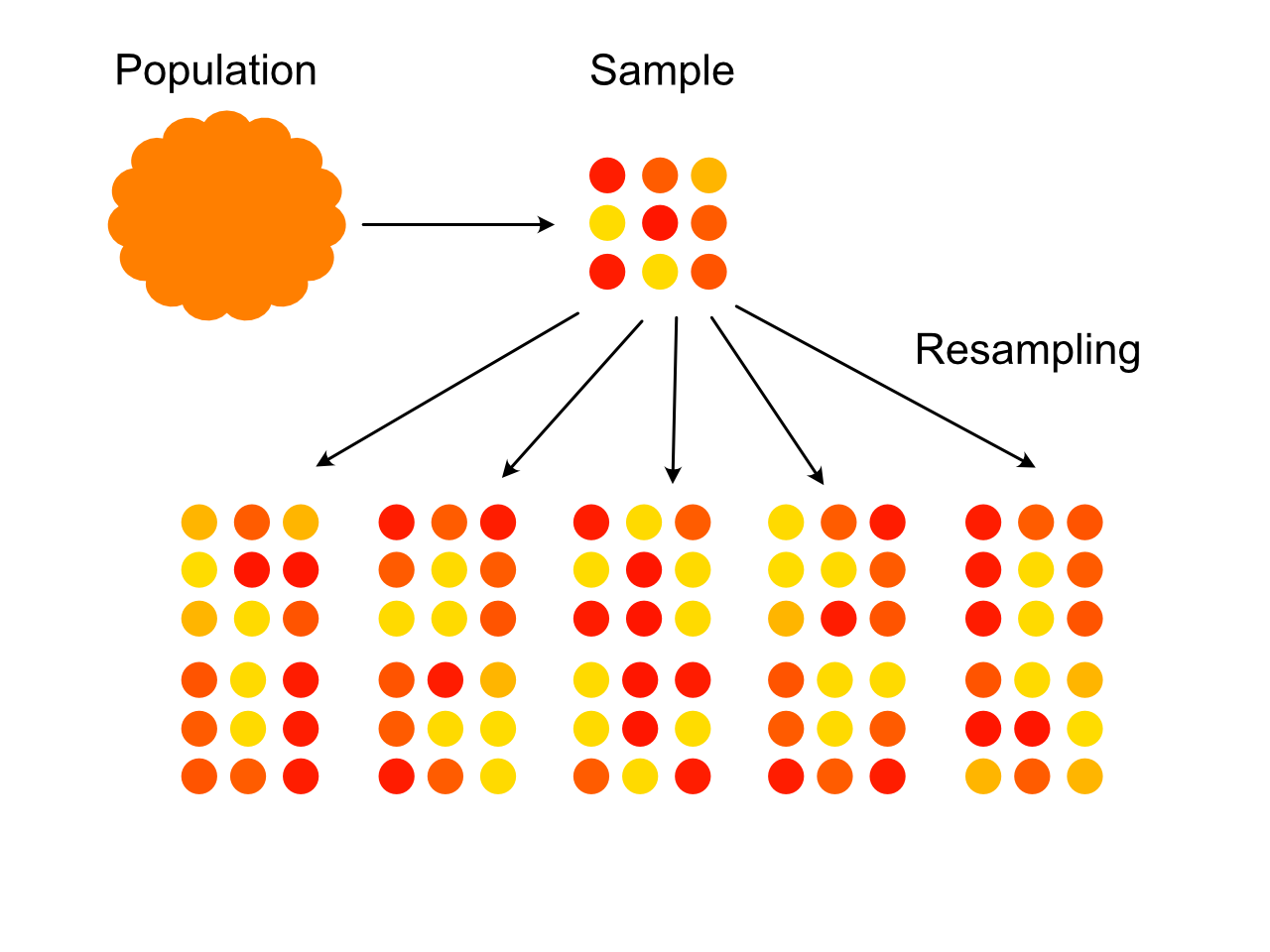
The Bootstrap
- Take a sample of size \(N\) from the population
- Compute sample statistic of interest \(S\)
- Randomly draw \(N\) observations with replacement from the original sample.
- Compute sample statistic \(S^*\) for this new sample.
- Repeat 2 - 4 many times.

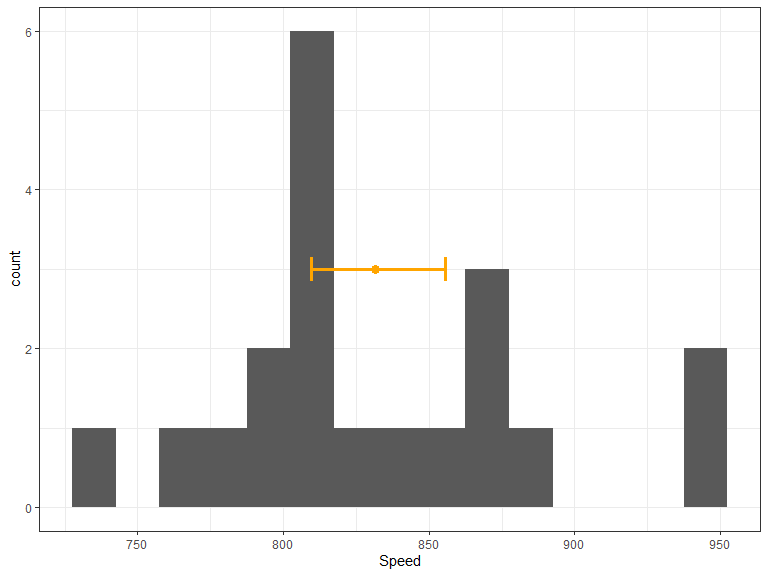
Example: The speed of light
In 1882 Michelson and Morley measured the speed of light by timing a flash of light travelling between mirrors.
(reported here in km/s - 299,000)
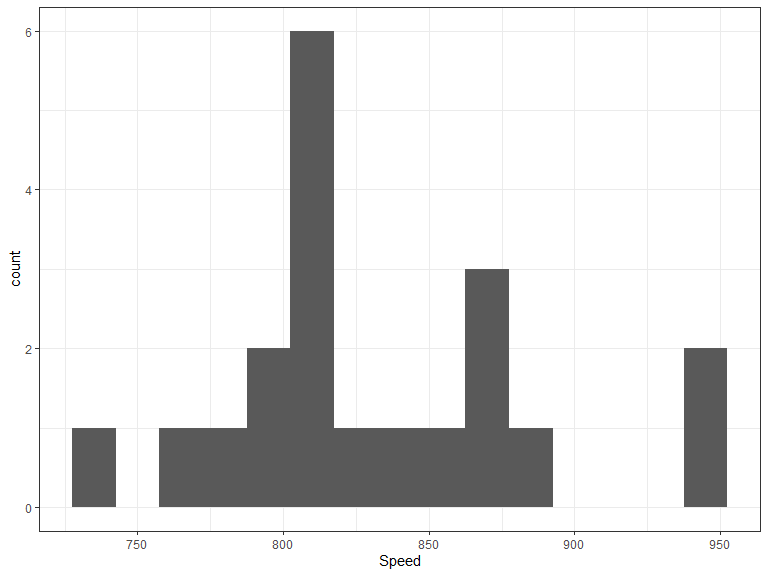
Estimating the speed of light
- 20 measurements taken
- Average observed speed of light is 831.5
- What would a 95% confidence interval look like?
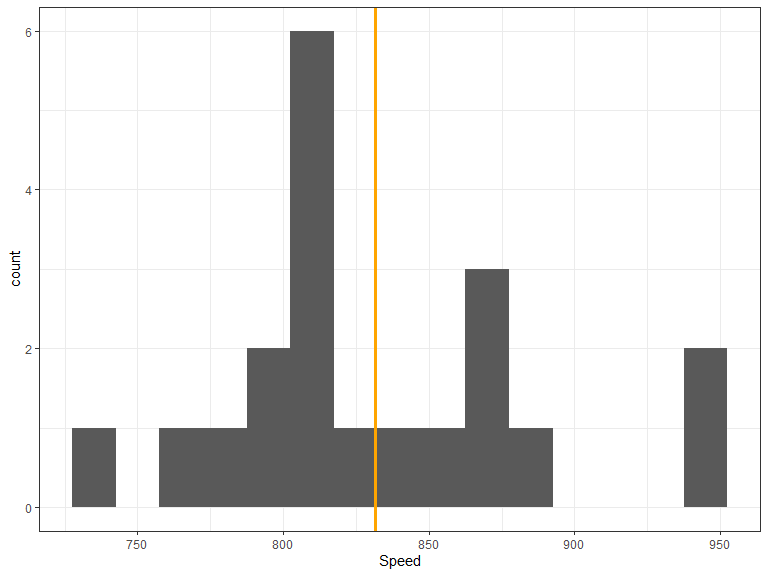
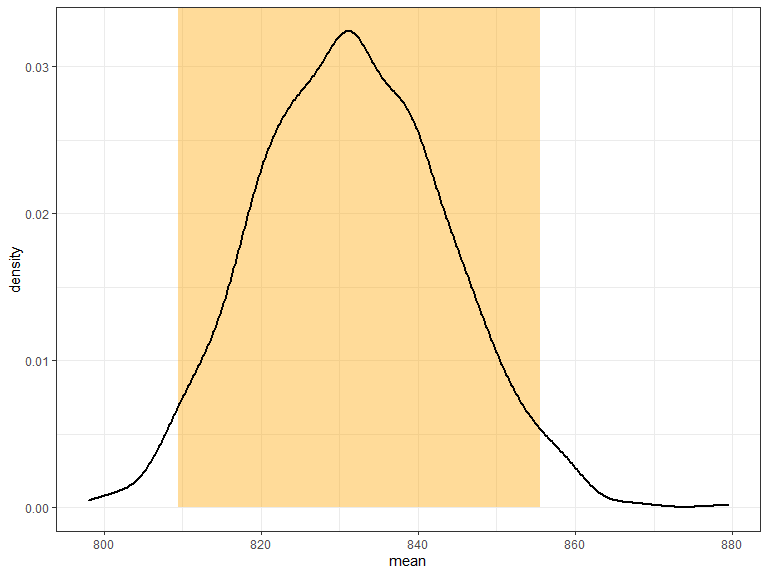
Bootstrapping a confidence interval
- Sample from the data (again and again and again)
- Compute the mean for each sample
- Use the 2.5th and 97.5th percentile of all means as bounds of the confidence interval
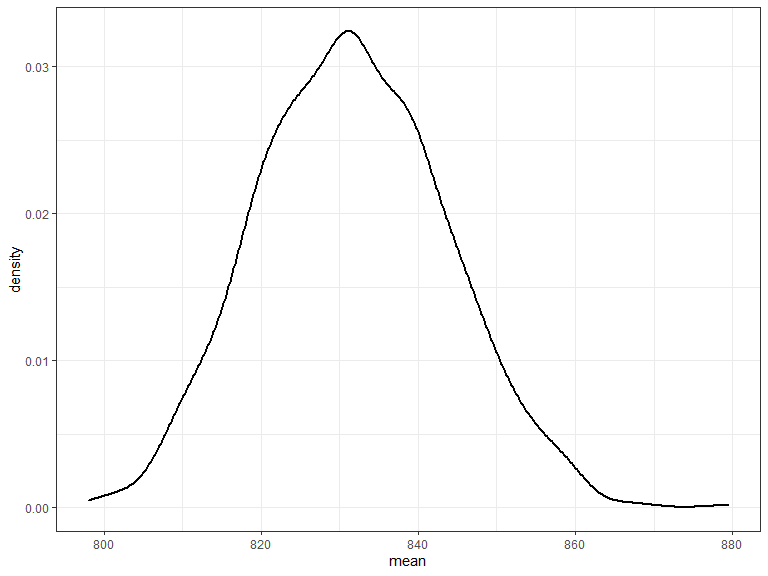
Bootstrapping a confidence interval
- Sample from the data (again and again and again)
- Compute the mean for each sample
- Use the 2.5th and 97.5th percentile of all means as bounds of the confidence interval
Bootstrapping a confidence interval
- Sample from the data (again and again and again)
- Compute the mean for each sample
- Use the 2.5th and 97.5th percentile of all means as bounds of the confidence interval
Null Hypothesis Testing
- What if we want to test for statistical significance?
- For example, is the speed of light estimate by Michelson & Morley significantly different from the current estimate?
- On the scale used here the speed of light is 792.5.
- Our estimate from the data is 831.5
- How likely are we to see an observation that is at least 831.5 - 792.5 = 39 away from the mean?
A bootstrap estimate of the p-value
- Bootstrap distribution of means is centred on observed mean.
- This is based on the observed data, i.e. not the null distribution
- Use this to approximate the null distribution.
- Calculate p-value based on number of bootstrap samples at least as far from the null as the observed mean.
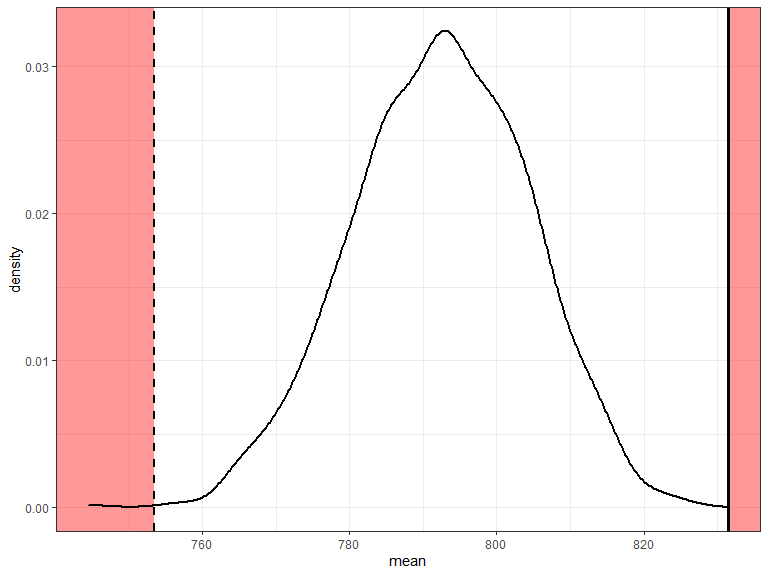
p = 0.001
A better bootstrap
- Assuming that we can just shift the distribution of the mean to obtain the null distribution may be questionable.
- Can we do better?
- Several variants of the bootstrap exist
- One possible improvement: Studentized Bootstrap
- Instead of using the mean of each sample, use a t statistic
Studentized Bootstrap
- Instead of using the sample mean \(\bar{x}\) use the t statistic \(\frac{\bar{x} - 792.5}{\hat{\textrm{se}}}\)
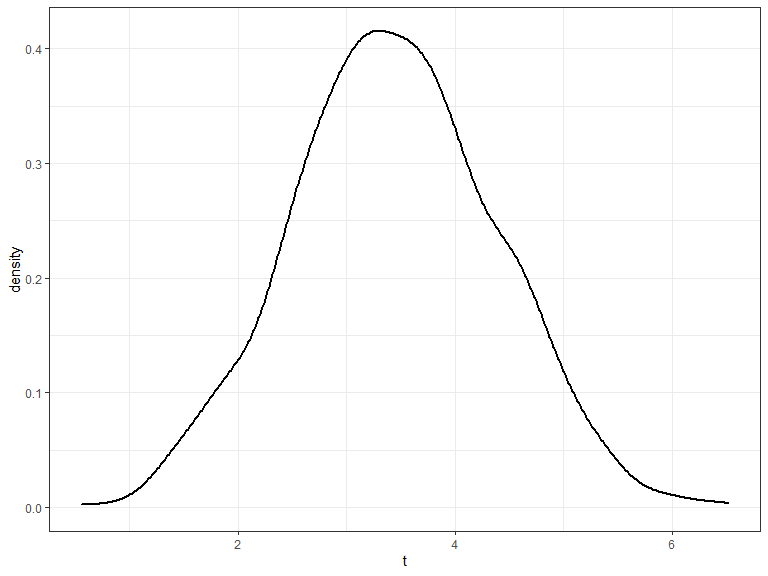
Studentized Bootstrap
Instead of using the sample mean \(\bar{x}\) use the t statistic \(\frac{\bar{x} - 792.5}{\hat{\textrm{se}}}\)
Then proceed as before
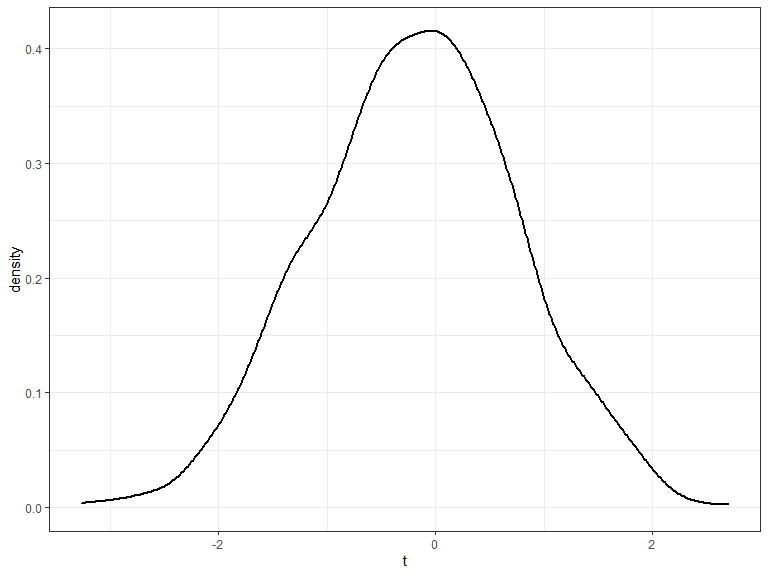
Studentized Bootstrap
Instead of using the sample mean \(\bar{x}\) use the t statistic \(\frac{\bar{x} - 792.5}{\hat{\textrm{se}}}\)
Then proceed as before
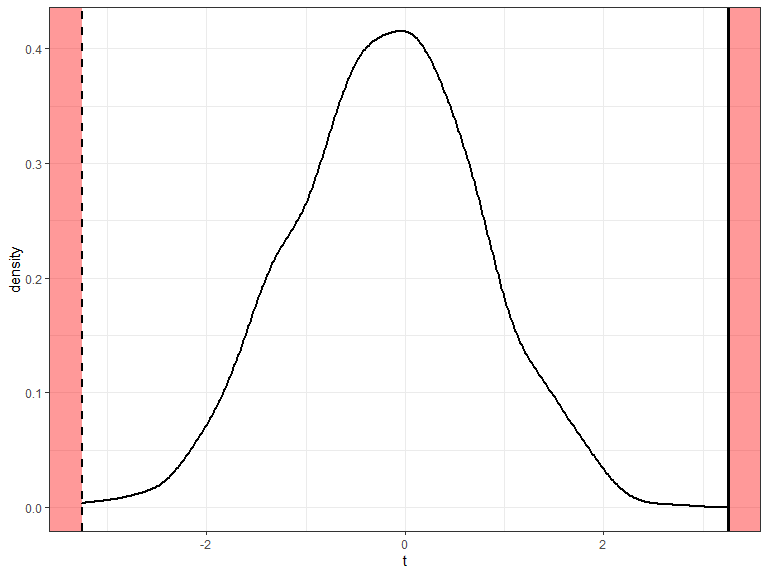
p = 0.001
Some things to consider
- How do we get the estimate of the standard error?
- Bootstrapping!
- Generate bootstrap samples for each bootstrap sample
- Gets time consuming pretty quickly
- Why is it better?
- Less sensitive to outliers
- Better approximation of null distribution
General considerations
- These bootstrap methods work best when
- the bootstrap distribution is symmetric
- centred on the sample estimate
- the sample isn’t too small
- The bias-corrected and accelerated (BCa) bootstrap is better at handling more difficult situations.
- Consider the structure of your data when resampling
How do I do this myself?

SPSS
- Options for bootstrapping are built into many analysis functions
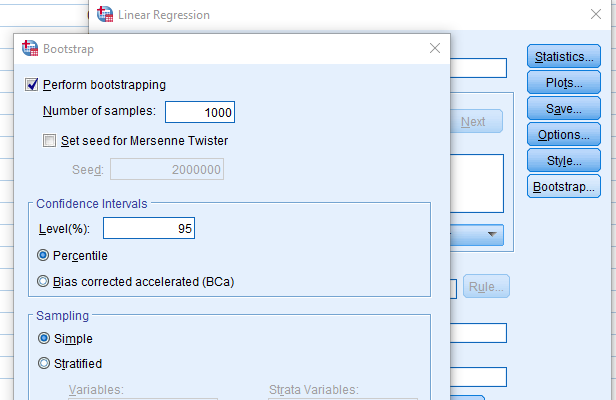
R
Many options, pick the one that’s right for you
- Package boot for general purpose bootstrapping
- supports time series and censored data
- Bootstrap linear model fits with package simpleboot
- lme4 has function
bootMer()for mixed models
SAS
- Use DATA step or SURVEYSELECT procedure for resampling
- Then use BY-group processing to obtain bootstrap estimates
Stata
- bootstrap command
Thank you
